Degenerate energy levels
In physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more than one linearly independent eigenstate with the same eigenvalue. Conversely, an energy level is said to be degenerate if it contains two or more different states. The number of different states at a particular energy level is called the level's degeneracy, and this phenomenon is generally known as a quantum degeneracy.
In quantum theory this usually pertains to electronic configurations and the electron's energy levels, where different possible occupation states for particles may be related by symmetry. For example, in the hydrogen atom, for a fixed energy eigenvalue, there exist several states which have that energy, but differ in the eigenvalues of angular momentum 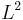 , spin component
, spin component 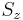 and so on. The usage comes from the fact that degenerate eigenstates correspond to identical eigenvalues of the Hamiltonian. Since eigenvalues correspond to roots of the characteristic equation, degeneracy here has the same meaning as the common mathematical usage of the word.
and so on. The usage comes from the fact that degenerate eigenstates correspond to identical eigenvalues of the Hamiltonian. Since eigenvalues correspond to roots of the characteristic equation, degeneracy here has the same meaning as the common mathematical usage of the word.
If the symmetry is broken by a perturbation, caused, for example, by applying an external magnetic or electric field, then the energies of the states can be changed, causing energy level splitting.
In electromagnetics, degeneracy refers to modes of propagation which exist at the same frequency and longitudinal propagation constant. As an example, for a rectangular waveguide, the TEmn mode is degenerate to the TMmn mode if m and n are the same for both of them.